Public key cryptography is one of the central technologies in securing communications across a myriad of scenarios, but especially through the internet. RSA, named for Rivest, Shamir and Adleman, who first publicly described it in 1978, is the canonical example of a public key crypto system, and is closely related to a number of other protocols such as Diffie-Helman. Its security is based on two key ingredients; perfect implementation of the pure mathematics that specifies the algorithm (such that no side information is available) and an assumption about the difficulty of performing certain calculations. In fact, the difficulty assumption is already known to be false. At this moment in time, we lack the hardware, a quantum computer, to exploit it, but such a realisation is inevitable. Thus, the security of RSA is rather based on the hope for a slow pace of technological development, which is hardly borne out by recent history. Moreover, it means that any information that is not time sensitive should not be encoded using RSA today.

RSA is an asymmetric system where one person, Alice, creates a public/private key pair, and makes the public component freely available so that anyone wanting to send her a message can encode it. However, only she, making use of her private key, can decode the result. Mathematically, this is based on modular arithmetic, in which we write a (mod b)=q to mean that a is divisible by b with remainder q. There are a variety of techniques, such as the Chinese Remainder Theorem and Euclid’s algorithm, that allow one to manipulate these expressions very efficiently. The core of RSA, however, is the use of Fermat’s Little Theorem, which enables the decoding process. It states that for a prime P, and an integer M

This is where quantum computers come in. While nobody has ever found a better way to factor on a regular computer, such a method has been found on a quantum computer. What makes a quantum computer different to the “classical” computers of our every day experience is, in essence, the software that they can run. Any program that can be written for a classical computer can be expressed in terms of a small number of elementary operations, or gates, with only a relatively modest overhead. The typical example is that of the NAND gate. By wiring up the inputs and outputs of a bunch of these gates, you can replicate any software program. The trick that new, quantum, hardware potentially allows is the addition of an extra gate to its toolkit that cannot be expressed in a nice way by the existing set of gates. Once the hardware that implements this new instruction set is available, the extra gate allows some subroutines to be rewritten in completely novel ways to gain massive speed advantages.

Although NAND gates are sufficient to replicate any classical algorithm, they are not reversible (meaning that you can’t, by looking at the output, figure out what the inputs were). This is fairly obvious given that there are 4 possible inputs but only 2 outputs. Now that we’re about to delve (superficially) into the world of quantum mechanics, in which every operation (except measurement) is reversible, it’s better to think of a different set of gates. Any classical algorithm can be rewritten in a reversible manner, and, having done that, it can be expressed as a circuit of only Toffoli gates . Any quantum computation can similarly be written as a circuit composed of two different types of gate – the Toffoli and the “square root of NOT”. The reason why the classical theory of computation seems self-evident, self contained and did not immediately lead to the insights of quantum computation is that one can argue this square root of NOT gate is impossible! To see this, a brief diversion is required. Consider a single bit, which takes values either 0 or 1. A simple operation on this bit is to flip its value, so if it’s initially 0, it ends up as 1. 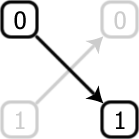This is the familiar NOT gate. More generally, it would seem reasonable to assume that any operation on this single bit can be described by the set of probabilities p_ij, which specify the probability of an input bit j being converted to an output bit i. 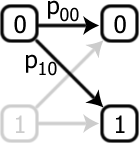The question is the following: is there any such gate that creates the NOT gate by two consecutive applications? 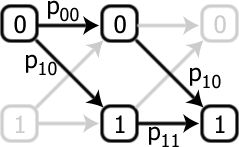One can calculate, for example, that the probability of converting from an input 0 to an output 1 is p₁₀(p₀₀+p₁₁), which we would need to equal 1. There are 3 other conditions, and given that probabilities can’t be negative, it is impossible to simultaneously satisfy all four. Hence, it is impossible to build a device which, by acting twice, gives the NOT gate. Since it is impossible to find a satisfying assignment of the probabilities, this gate is said to be logically impossible. The only problem is the inescapable fact that such an operation, which we call the square root of NOT gate, does exist! The resolution is that while the axioms of probability seem obvious from our daily experience, there is no fundamental rule that says they have to be obeyed and, indeed, when one enters the quantum-mechanical regime, the statistics obey a different set of axioms.

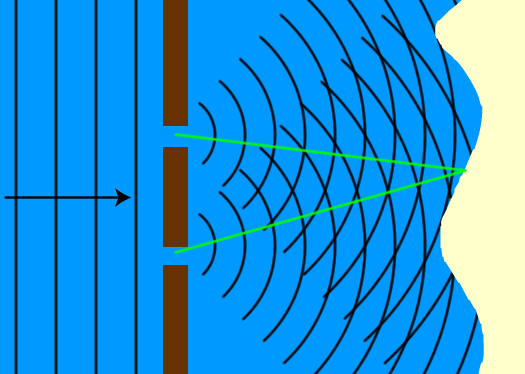
How does this contribute towards a new algorithm for factoring numbers? It opens up new avenues of investigation because this square root of NOT gate allows us to (crudely speaking) evaluate a function for many different inputs simultaneously. While we can’t just read out all those sets of values any faster, we can ask about some global properties of those values. The simplest example is a one bit function evaluation where you want to know whether f(0) and f(1) are the same or different. Classically, we would have to evaluate both f(0) and f(1) separately, and then compare the two answer bits. Quantumly, however, this is not necessary. If this sounds strange, it’s worth realising that even classical waves exhibit similar properties. Imagine a water wave coming in and hitting a wall, in which there are two holes. From the other side of the wall, this will look like two new waves, one emanating from each hole. The height of the water at any given point is just the sum of the heights of the two waves, so if two peaks coincide, the water is much higher. The maximum height that the water achieves at a given point depends on when the peaks of the two different waves arrive. However, it doesn’t depend on the two arrival times independently. Instead, it depends on the difference between their two arrival times, i.e. there is information about the difference in the distance of the point of observation from the two different holes. It’s exactly these sorts of differences that we can probe with quantum states (except that different, quantum mechanical, probability axioms apply, meaning that wave heights don’t simply add. Sometimes, they can subtract!).

Figure 1 is a photo of an experiment that is composed of two partially reflecting mirrors (bottom left and top right) and two normal mirrors (top left and bottom right). The normal mirrors are just there to help with the routing of the light, and are otherwise irrelevant. Each of the partially reflecting mirrors can be thought of as a logic gate. There are two sides (left, bottom) which are inputs and two which are outputs. We can label the inputs as 0 and 1, and label the outputs such that if light is inputted for a given logical value, and happens to be transmitted, the output site corresponds to the same logical value. With two of these mirrors chained together, the overall output is the NOT gate, so a single mirror is this square root of NOT that is claimed to be impossible. Fire a photon in to 1 input and it always comes out at the 0 output. It helps to think of the light passing through the system as a wave. After passing through the first piece of glass, this wave travels along both possible paths, and then recombines at the second piece of glass. How it recombines depends on the relative positions of the peaks of the two waves. The two paths are exactly the same length, so the only thing that can create a relative shift between the peaks of the two waves are whether those waves were transmitted or reflected on the partially silvered mirrors. In the case where we look at the opposite output to the input (e.g. input 1, output 0), the waves along both paths get reflected once and transmitted once. Thus, they have the same change in peak position, and the peaks arrive together. They combine together so that the photon appears on that output. If the photon appears there, it doesn’t appear in the other output. Without introducing a whole lot of mathematical notation, we’re quickly running out of suitable words to describe what’s going on, simply because quantum mechanics’ operating regime is so far outside our day to day experience. Nevertheless, the idea is simple; there are operations that cannot be described by our usual logic, and by extending the set of available operations we can recode some sub-routines to operate more quickly, particularly if the answers we’re after depend on global properties of a function. It’s not a magic solution that means everything will run faster, but some specific instances will be able to benefit. It is worth emphasising that while quantum mechanics is famed for its weird probabilistic actions such as a cat being both dead and alive at the same time, quantum computers actually operate (almost) deterministically. While they might go through strange intermediate configurations that are the equivalent of the dead and alive cat (or a single photon passing through both paths at once, evaluating both functions), the whole game of designing quantum algorithms is still to give a definite answer at the output.

Factoring is one instance which benefits from the extended set of operations because it can be cast into an equivalent problem known as order finding, which demands a global property of a function (based on the Fourier Transform). In order to factor the number PQ, start by picking a random number x which is less than PQ. Assuming x is does not share a common factor with PQ (in which case, we’d be done already), then the order, r, of x is defined to be the smallest integer such that xr (mod PQ)=1. A little number theory can be used to prove that r is almost certainly even. That means that it can be written as $$(x^{r/2}-1)(x^{r/2}+1) ({\rm mod} PQ)=0$$ In other words, $(x^{r/2}-1) ({\rm mod} PQ)$ must be a multiple of either P or Q, from which the factors can be extracted . Hence, our only goal is to find r. To do this, it is worth realising that for any integer k=ar+b, $$ x^k ({\rm mod} PQ)=(x^r ({\rm mod} PQ))^a(x^b ({\rm mod} PQ))= x^b ({\rm mod} PQ) $$ So, the function f(k)=x^k (mod PQ) has a repeating pattern with period r. It is exactly this periodicity that a quantum computer can take advantage of. We can write a quantum sub-routine that evaluates f(k) for all different k, and examines the periodicity, thereby extracting r. In practice, all it extracts is the closest integer to the value 2Ls/r, where L is a parameter that we specify (it grows linearly with the number of bits of PQ), and s is an unknown integer. Another standard algorithm, known as continued fractions, comes to the rescue and guarantees to extract from this value the numbers s and, most importantly, r. So, the majority of what we do uses standard classical algorithms, simply substituting a new (quantum) subroutine for finding the order in the middle. This is the major step, however, and reduces the running time for factoring an n bit number down to a time that scales with n³.

It is this reduction in the scaling associated with the factoring algorithm that makes RSA unreliable. It is not the same as a one-off speed boost arising from building a faster processor. Even if we suddenly made a processor 1000 times faster, RSA could simply compensate by using a few more bits. However, with this different scaling, calculating the private key from the public key takes a similar time to all other calculations required in the legitimate application of RSA. Not only is it infeasible to create a sufficiently large key to exclude an eavesdropper on the basis of insufficient computational power, but doing so would also exclude legitimate users from performing the message encoding, decoding etc. because they would have insufficient computational power.

For now, we’re safe because the hardware to implement these quantum computations doesn’t exist yet. While the theory of what is required of a quantum computer is well developed, experiments are still in their infancy, only operating on a few qubits. Nevertheless, from the moment the first quantum computer is turned on, all messages previously encoded with RSA will be readable. Any secrets that need to remain so after that moment, whether it comes in 10 years or next week, should not trust RSA now. Security based on the assumption of the lack of technological progress hardly constitutes security.

If RSA can’t be trusted, what should we use instead? Two natural candidates present themselves. The first is quantum cryptography, which replaces the assumption of computational intractability with one about the physical nature of the Universe, which seems a much more secure footing, but requires hardware working in the quantum mechanical regime. Still, this hardware is much simpler than that required for breaking RSA, and some systems are already available commercially. The second option would be to remain with a classical public key crypto system, but one which we don’t believe can be broken by a quantum computer. The logical starting point for this may be to base it on a so-called “NP-complete” problem; the class of the hardest problems for a classical computer to solve for which the solution can be easily verified (the verification step is equivalent to Alice producing the public key from her private key, and solving the problem is equivalent to the eavesdropper trying to produce the private key from the public one). It is not known that quantum computers can efficiently solve these, and it is generally believed that they can’t. If true, then this would recover the exponential scaling, and hence place the possibility of reverse engineering the private key from the public one beyond even the scope of quantum computers, but still leaving the basic implementation for legitimate users on a classical computer. No such system exists yet. One of the sticking points seems to be that proving that a problem belongs to this general class is based on the worst case – there only needs to be one instance of a function evaluation that is difficult to compute, while most cases could be easy. In comparison, for a crypto scheme to be reliable, it would have to utilise a subset of instances which are all hard to compute. While this has not been proven for any of these hardest of problems, there are cryptosystems based on finding distances between points of a lattice, which involve functions that are not known to be attackable by quantum computers. This lattice-based cryptography is a strong candidate for an immediate replacement to RSA.

Alice releases two public components, PQ=77 and e=13. She keeps secret the values P=7, Q=11 and d=37. Bob wants to send Alice the number 42 secretly, so he calculates 4213 (mod 77)=14, and sends that instead. When Alice receives 14, she calculates 1437 (mod 77)=42, correctly recovering the intended message.

In this instance, it is very obvious what the factors of 77 are. Instead, we proceed by selecting a value which is coprime with 77, such as x=5.

n	1	2		15		29	30	31	32
5n (mod 77)	5	25	…	34	…	31	1	5	25

From this, we can identify that the sequence repeats with period r=30, which is even. Hence x^r/2-1 (mod 77)=33. Via Euclid’s algorithm (or inspection), the highest common divisor of 33 and 77 is clearly 11, one of the factors. From this, the other factor, 7, is recovered, and a suitable d is calculated.

Side Information: Even if the pure mathematics of an algorithm can be proven to be perfectly secure, the translation from that ideal specification into a practical protocol can reveal additional, side, information to an adversary that can be used to break it. For example, the time it takes to perform a certain operation must be the same for all possible inputs otherwise the time required conveys something about the input.

Euclid’s Algorithm: When presented with two integers, Euclid’s algorithm is a very quick and simple method for finding the largest number that divides into both integers, i.e. it finds the largest common factor.