The problem
In a room there are 100 people, numbered from 1 to 100. A person is either a knight or a spy. Knights always tell the truth, but spies may tell the truth or lie as they see fit. Every person in the room knows the identity of everyone else. It is given that strictly more knights than spies are present.
Asking only questions of the form ‘Person i, what is the identity of person j?’, what is the minimum number of questions which will guarantee to find everyone's true identity?
Background
I heard this problem from Dave Johnson. Some time after publishing a solution I learned from Tim Chow that Pavel M. Blecher had already published a similar solution: see On a logical problem, Discrete Math. 43 (1983) 107-110.
The problem was asked on Puzzling.stackexchange.
Variants with a smaller number of people, but with a greater variety of questions allowed, are well known, and seem to have first been considered by Raymond Smullyan. The end of Mark Newheiser's webpage suggests that 500 questions should suffice. Before continuing, the reader might care to find a questioning strategy that meets this target.
An easier exercise, which still gives a good flavour of some of the arguments needed for the
general problem, is to show that five more questions suffice
to find all the identities in the nine person room shown below. Seven
questions have already been asked:
red arrows indicate accusations, green arrows supportive statements.
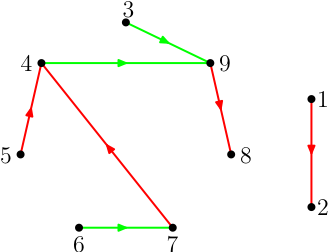 Hint: try to resolve the identity of Person 9, using that at most four spies are present.
Hint: try to resolve the identity of Person 9, using that at most four spies are present.
Solution
My paper starts by giving the Spider Interrogation Method which guarantees to find everyone's true identity in at most 148 questions. In general, if there are n people, then the number of questions used by this method is very slightly less than 3n/2.The harder part is to show that, no matter which method one uses, it will in the worst case require at least 148 questions.
Consider the following two-player game. Player 1, the Interrogator puts a question, in the usual form to Player 2, the Secret Keeper. The Secret Keeper considers the various ways in which knights and spies can be arranged in the room that are consistent with his or her answers so far, and then supplies the answer: ‘Knight’ or ‘Spy’. The Interrogator's job is to nail down everyone's identity as quickly as possible. The Secret Keeper's job is to play the role of malign fate, and force the Interrogator to ask as many questions as possible.
Note that the Secret Keeper is not committed, even secretly, to any particular arrangement of knights and spies. All that matters is that, at every point in the game, there is a way to assign identities to the people that is both consistent with his or her answers, and leaves spies in a strict minority.
The diagram below shows an example game in a six person room after the Interrogator
has put four questions, and the Secret Keeper has given four replies.
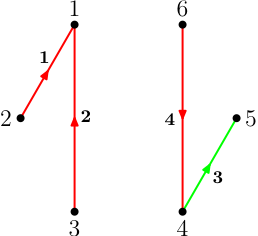
The Secret Keeper's fourth reply was a blunder, for after it the Interrogator (who knows that at most two spies are present) can now be sure that Person 1 is a spy, and that either Person 4 or Person 6 is the remaining spy. The Interrogator can therefore find all the identities in just one more question. If, however, the Secret Keeper had given the reply ‘Knight’ on his or her fourth turn then the Interrogator would have been held to 7 questions. This, is in, fact the smallest number of questions that will guarantee success in a room with 6 people, so both players have then played optimally.
The problem can therefore be rephrased as finding an optimal strategy for the Secret Keeper. My paper gives two such strategies: Knight Hiding (which is arguably the obvious greedy strategy) and Knavish Dividing (which has the interesting feature that the spies turn out to lie in all their answers).
Finding a knight
Suppose instead the aim is to find one person who must be a knight. This problem was first solved by M. E. Saks and M. Werman, On computing majority by comparisons, Combinatorica 11 (1991) 383–387 in the case of spies who always lie.
A solution in the general setting where spies are (as usual) unconstrained, and it is known at most s spies are present, for some s < n/2, was given by John R. Britnell and me in this joint paper.
Finding a spy
Another interesting searching game arises if it is known that a spy is present, and the aim is to find one. This paper solves the problem and a number of variants. The two computational claims in the final section of the paper are checked by the code below.- MajorityGame.hs. Finds values of positions in the majority game.
- AllMajorityGame.hs. Finds values of positions in the majority game when the aim is to determine all identities.
- Main.hs. Used to produce the data in Section 8.1 and to check Conjecture 8.3.
Open problems
(1) Better performance on average
It is natural to ask whether there is a questioning strategy which will guarantee to use at most 148 questions to find all identities in a 100-person room, and will with high probability use fewer, no matter how cleverly the spies answer.
The Chain
Building Method, which aims to form long chains of people all vouching for
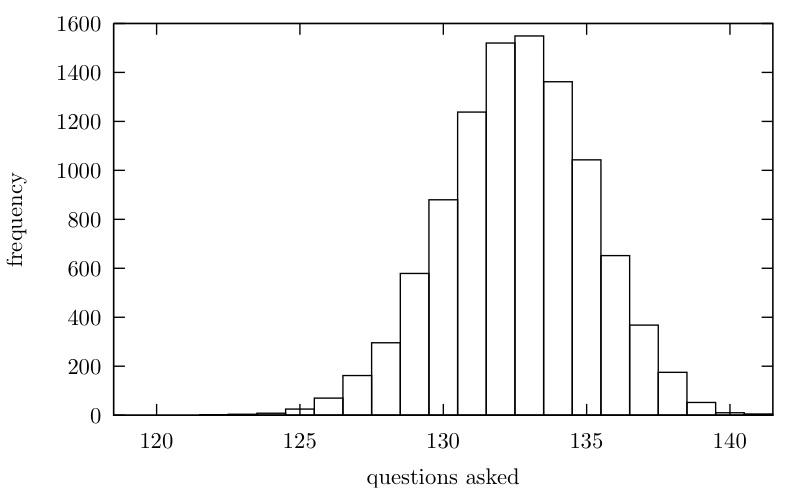
one another, appears to be such a strategy. Numerical evidence suggests that this
method will usually use just over 130 questions to deal with a room in which knights
are just in the majority, while never using more than 148. This however remains
to be proved. The graph below shows a typical distribution of questions.
A refinement of the Spider Interrogation Strategy proves that a related question has an affirmative answer. The result in this note is stated without proof in my original paper.
(2) Knights and spies for logicians
Fix a propositional formula, for example p OR q. The questioner is now allowed to go up to any person and ask them to state their view on a specialisation of this formula. For instance, he could ask person 1 ‘is either person 2 or person 3 a knight’. (Of course, if person 1 is a spy then he can answer as he sees fit.) Formulae with implication signs raise an interesting difficulty, for if a knight is asked ‘would person 2 support person 3’, it is unclear how he should answer if person 2 is a spy. On the other hand, if asked 'is either person 2 a spy, or person 3 a knight', he will have no problems.Other computer programs
Experience of real-life games suggests that it is all too easy for the Secret Keeper to inadvertently answer in such a way that all consistent interpretations of his or her answers require spies to be in the majority. Here is the source for my Haskell program ‘Gamechecker’ that will check whether a game is in a consistent state. (The first line gives basic instructions on how to use it in ghci.)
Some old Objective-C code for simulating a variety of questioning strategies
is available here.
Seminar
The slides from my talk at the Bristol Algorithms Days, Feasibility Workshop, February 2010, are here.