Mark Wildon's Website: Other Mathematics

People

Dave Benson, Christine Bessenrodt, Simon Blackburn, John Britnell, Peter Cameron, Anton Cox, David Craven, Charles Eaton, Karin Erdmann, Matt Fayers, Eugenio Giannelli, Nick Gill, Simon Goodwin, Jan Grabowski, Anne Henke, Sinead Lyle, Paul Martin, Andrew Mathas, John Murray, Nikolay Nikolov, Rowena Paget, Alison Parker, Sarah Rees, Jeremy Rickard, Sibylle Schroll, Peter Symonds, Matt Towers.

Recent talks

Foulkes' Conjecture and plethysms

Let m and n be natural numbers. The Foulkes character for m and n is the permutation character of the symmetric group of degree mn given by its action on the collection of all set partitions of a set of size mn into n sets each of size m. Foulkes' Conjecture states that if m < n then the character for the action on m-subsets contains the character for the action on n-subsets.

Data on Foulkes multiplicities

Proposition 5.1 in this paper with Rowena Paget and Anton Evseev gives a new recurrence for the character multiplicities in Foulkes' Conjecture. Using this recurrence we extended earlier work by Jurgen Müller and Max Neunhöffer to prove Foulkes' Conjecture whenever the parameters m and n satisfy m + n < 20 and, later in 2016, to m + n ≤ 20.

The graph below shows the differences between the base 2 logs of the multiplicities of irreducible characters labelled by partitions of 56 in the Foulkes characters for m = 7, n = 8 (larger multiplicity) and m = 8, n = 7 (smaller multiplicity).

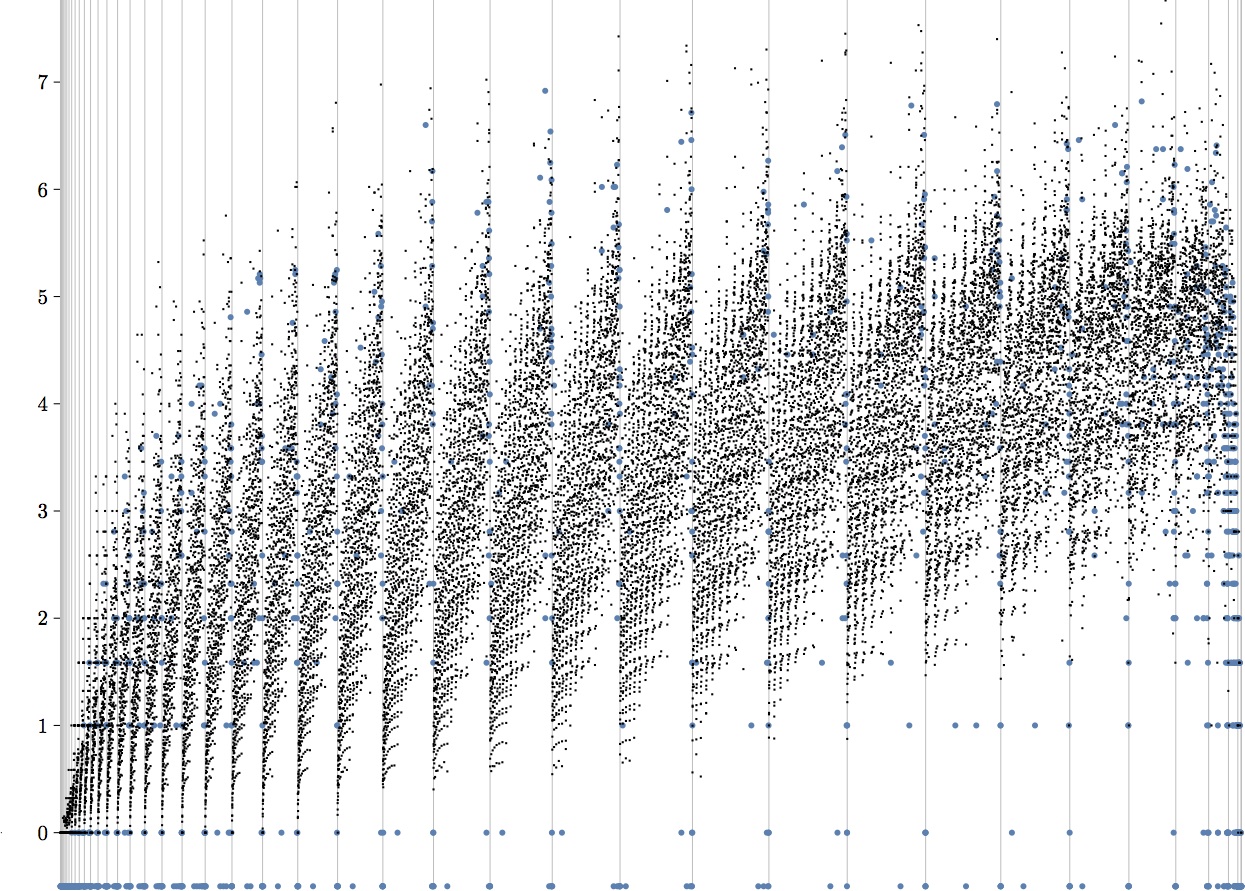
The 31275 partitions of 56 with at most 7 parts are ordered lexicographically: blue dots show multiplicities where the multiplicity in the smaller character is 0. If both multiplicities are zero the dot is drawn below the axis. Vertical lines show changes in the largest part of the partition.

Minimal constituents of Foulkes characters

The links below give some supporting material for this paper with Rowena Paget.

  • SetFamilies.hs. Haskell source code for computing minimal constituents of Foulkes characters using Theorem 1.2 of the paper.
  • Examples.hs. Verifies two of the counterexamples presented in the paper.
  • Minimals.txt. Minimal constituents of Foulkes modules for m and n such that m + n < 20

Minimal and maximal constituents of generalized Foulkes characters

This paper with Rowena Paget describes all minimal and maximal constituents of the generalized Foulkes characters corresponding to the plethysms sν ○ sμ where ν and μ are arbitrary partitions.

  • TableauFamilies.lhs. Literate Haskell code generating the conjugate-semistandard tableau family tuples that parametrize these constituents. It may also be used to check Example 8.3 and perform Algorithm 9.5.
  • Source code (compiled by LaTeX).

Littlewood's third method

If there is a unique symmetric function f such that 〈f, s(3n)〉 = 1 and 〈f, s(1) sλ〉 = 〈s(n-1) ○ s(3)) s(2), sλ〉 for all partitions λ of 3n-1 then, as Littlewood observed on page 349 of this paper, this f is the plethysm s(n) ○ s(3). The Haskell source code linked to below shows there is a unique f for n ≤ 8 and so Littlewood's method is effective in these cases. (Evaluate claimInPaper at the Haskell prompt.)

Plethysms of symmetric functions and representations of SL2(C)

Let E be the natural representation of SL2(C). In this paper with Rowena Paget we study when the representations ∇λ SymrE and ∇μ SymsE are isomorphic. Equivalently, when are sλ(1,q,…ql) and sμ(1,q,…qm) equal up to a power of q?

  • HookContent.hs. Haskell source code for searching for isomorphisms and checking the classification in Section 10.
  • Main.hs. Use to compile HookContent.
  • ExceptionalEquivalences.nb. Mathematica notebook that can be used to verify the exceptional isomorphisms in Section 11.

Involutive random walks

The involutive random walk on the set {0, 1, … n - 1}, started at the state x chooses y ≤ x according to a prescribed probability distribution, and then steps to n - 1 - x. These walks have a remarkably rich theory explored in this paper.

Simplex homology

Magma code for checking the base cases in Theorem 1.1 and conjectures in Section 7 of my paper The multistep homology of the simplex and representations of symmetric groups.

Burnside's method

A group K is said to be a B-group if whenever K is a regular subgroup of a permutation group G then G is either 2-transitive or imprimitive. Burnside proved that Cp is a B-group whenever p is prime. He later published two papers attempting to extend this result to other abelian groups. Both have fatal but interesting flaws. A proof of Conjecture 6.5 in my linked paper will rescue Burnside's proof for cyclic groups of even order.

  • RamanujanMatrix.hs has been used to verify Conjecture 6.5 for permutation groups of degree at most 600.

Coherent subgroups of permutation groups

Let G be a permutation group acting on a set Ω. We say that G is join-coherent is the set of orbit partitions of elements of G acting on Ω is closed under the lattice operation of taking joins, and meet-coherent if it is closed under taking meets. These definitions were introduced in this paper with John R. Britnell.

Conjugacy probabilities in finite groups

Let G be a finite group and let g and h be chosen independently and uniformly at random from G. Let κ(G) be the probability that g and h are conjugate, and let ρ(G) be the probability that g and h have conjugates that commute. The links below give some supporting material for this this paper with Simon R. Blackburn and John R. Britnell where we study these probabilities for symmetric groups and other finite groups.

  • KappaRho.hs and Main.hs. Haskell source code for computing κ and ρ for symmetric groups. Verifies all the computational assertions in the paper. See Main.hs for instructions.
  • KappaRhoValues.txt. Values of κ for symmetric groups of degree at most 100 (see OEIS A087132), and ρ for symmetric groups of degree at most 40 (see OEIS A192983).

Numerical data on derangements

Numerical data on derangements in symmetric groups acting on k-sets. In the linked table, the entry in position (n,k) shows the number of derangements in the symmetric group of degree n, its natural action on k-sets. The data are also available in plain text. Computed as part of joint work with John R. Britnell. This note describes the algorithm used and its implementation. Haskell source code:

Generalized Bell and Stirling numbers

This Magma code may be used to verify the claims in Section 7 of this paper with John R. Britnell.

Knights and spies

The Knights and Spies Problem has its own webpage.

Expository notes

Some notes on more basic mathematics are on my teaching page.