Links
Bristol maths. Oxford maths. Cambridge maths. MathSciNet.
Seminars in London: Pure Mathematics Seminar (at RHUL), London Algebra Colloquium (migratory), Information Security Group Seminar (at RHUL).
Seminars in Bristol: Algebra and Geometry Seminar, Heilbronn Seminar.
Seminars in Oxford: Algebra Seminar.
Oxford algebra group. BLOC homepage. Representation theory on the Arxiv. Trinity College. Part III courses. LaTeX tips.
Conformal
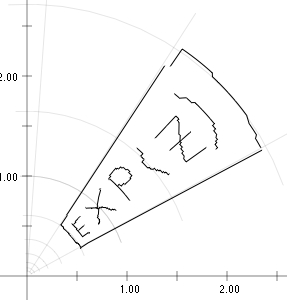
A program to help one visualise complex functions written when I was learning Objective C. Here is a screenshot. Here is a link to version 0.22 which should work on Mac OS X 10.6 and later. (For changes see here.)
I wrote this program after Matt Towers implemented the idea in Java: he has kindly given me permission to mirror his applet version here.
Haskell

Some links:
The picture on the left comes from my attempt at a Oxford Comlab practical on L-Systems.
Satire
- Playing soldiers (25th May 2000)
- Duke declares war on grey squirrels
- Slaughter of the innocents (3rd August)
- Compassionate conservatism
- Elgin Marbles
- Liberal Democrat earns money (7th August)
- A vicious game. Updated with the Dorneywood Rules Variation.
- Obit, Peter Birr
- Rodents take over house (14th August)
- Achieve success by adjusting your expectations
- The Silly Season (précis) (13th September)
- Come the millenium (8th November)
- The problem with satire (29th April 2001)
- Nuclear matters (5th Apr 2004)
- The Attentive Reader (1st Mar 2006)
- Pympyhllnynt cwrt y Abertawe (2006–2007)
- A mathematical proposal (25th Feb 2008)
- Canis Academicus (10th Oct 2008)
Short story
- Two days in the life of Prof. Orffbaron (April 2020)
Lockdown bread
- Wholemeal 75% hydration. My own recipe: 250g wholemeal, 250g water, 40g treacle, 50g sourdough starter, mixed up and left in fridge overnight. Then add 250g strong white, 150g water, 2 tsp salt, 15g pumpkin seeds, 20g sunflower seeds. (Also 1/2 tsp yeast if poolish doesn't have obvious bubbles and air when cut into it: usually it does.) Mix, turn three times for a minute or so with dough whisk at 20 minute+ intervals, overnight in fridge, stretch and fold for a minute, shape into boule, proof in well-floured banneton, turn out onto oiled baking tray, score top, bake 30 minutes at 240C and 15 minutes at 200C.


Update January 2021. Sprayed with water and then baked in a Dutch oven the crust is crisper and the crumb just slightly lighter. Remove top for final 5 minutes. Before I had used a tray of water in the main oven, but this seems far less effective at maintaining humidity. Tends to stick, but this can be averted with a disc of parchment paper.

- White sourdough 70% hydration. My own recipe: 200g strong white with 200g water, 40g sourdough starter, 1/4 tsp yeast in sponge for 9 hours.Then mix with 80g water, 200g strong white, 3/2 tsp salt (do not forget!), 1/2 tsp sugar (to brown the crust) and stretch-and-fold at 20 minutes intervals three times. Remainder of method as above. [Loaf below is 75% hydration, but 70% is safer.]




Update November 2021. With Dutch oven, intensive irrigation by spray bottle at 75% hydration and double scoring, one cut slightly deeper than the other.

Update July 2022. As above, but using only sourdough starter, with a 24 hour pre-ferment and 48 hour proof, baked 45 minutes to get crust very brown.

- Rye sourdough 83% hydration. Adapted from recipe on breadtopia: 180g strong white, 180g light rye, 300g water, 40g treacle, 40g sourdough starter, 1 tsp yeast, 3/2 tsp salt, 5/2 tsp fennel seeds, 1/2 tsp caraway seeds. Method as wholemeal but for best crust finish it off with an extra 5 minutes at 240C, and probably no need to reduce temperature.

